Modal Analysis of Non-Stationary Vibration

Introduction

In practical cases, the dynamic properties of engineering systems change with operational conditions, and these systems are known as non-stationary systems. Typical application areas include traffic-excited bridges, earthquake-excited structures, surface and sea vehicles, robotic devices, rotating machinery, and so on. It is more complicated to extract modal parameters of non-stationary systems than stationary systems whose dynamic properties remain constant with time [1]. Localized stationary methods for non-stationary systems are based on conventional stationary frequency domain or time domain system identification and signal segmentation techniques. In these methods, each segment is sufficiently short to warrant approximate stationary behaviour and the subsequent characterization of a non-stationary signal by a sequence of locally stationary models [2, 3], and direct functional time-varying parameters [4, 5]. This approach provides a tool for modelling abrupt signal changes of the non-stationary to mitigate the weakness of non-stationary methods.

Within the scope of this paper, a new algorithm is proposed to monitor the modal parameters. This method uses a short-time sliding window for an autoregressive model. In each segment, the Schur complement is applied to update the matrix inverse in the least-squares algorithm. This algorithm will allow for the updated parameters via time and the model order. The goal of this method is to avoid computing complexity and time consumption for the online slow varying monitoring of non-stationary cases. Consequently, this method inherits the practicability of the short time window technique and the accuracy of the autoregressive model, while improving model updating speed and versatility for better modal analysis and monitoring.

Real Vibration Application

To evaluate the fluid-structure interaction, a hydraulic test bench was designed and assembled at ÉTS in the Dynamo Laboratory. PCB330A sensors were used for vibration measurements. Six sensors were used in all our tests to record accelerations. Miniature pressure sensors were employed to record dynamic pressures applied on submerged structures due to flow. An acquisition box called Vishay System 6000 was used to record pressure sensors during different tests. The “Strain Smart” software was designed to work with the Vishay acquisition box and allows data to be exported and saved. A PCB impact hammer was applied to the structure in static tests. In order to hit the tested plate at different depths, the hammer was equipped with a steel extension. The experimental configuration is depicted in Fig.1.

Fig. 1. Photo images showing the experimental configuration

The tested structure was placed inside a perforated tank. Flow speed could be regulated with valves and different outlet nozzles. The fastening system used was a multitasking tool, which allows mounting a plate in different boundary conditions. Fig. 2 presents temporal response data at a sampling frequency of 1280 Hz. The tested steel plate measures 500 mm x 200 mm x 2 mm.

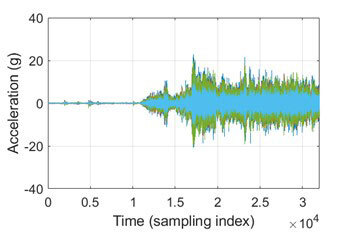
Fig. 2. The plate’s temporal response

The low amplitude portion corresponds to the submerged period while the high amplitude portion is attributable to the emergence of the plate from the water into the air. This shows that because of the fluid effect, the plate’s natural frequencies change with respect to the submerged depth. Before the plate rises, its modal parameters are both computed and identified using analytical and experimental methods at different depths, illustrated by depth on plate length ratio (D/L), as shown in Table. 1.

Table. 1 Modal identification of emerging plate

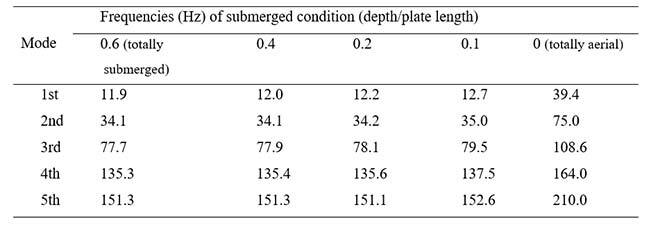
Fig. 3 shows the plate’s monitored frequencies under the proposed method. Frequency variations match the plate’s emergence, showing the slow change from the system still in the water to the abrupt change when it appears at the surface.

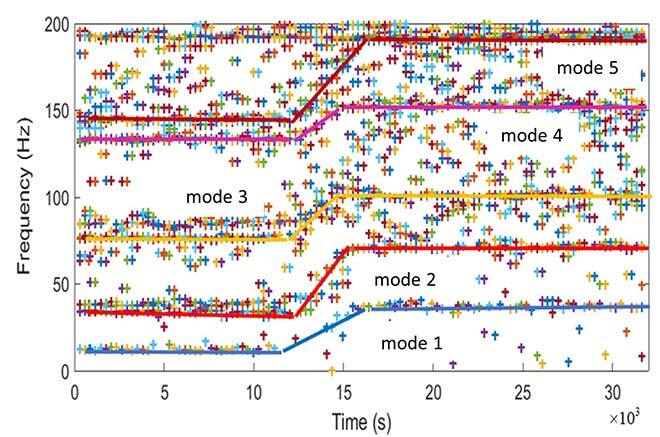
Fig. 3. Monitoring of the plate’s natural frequencies with the proposed method

We compared the calculated values in Table 1 with the data’s short-time Fourier transform plotted by the channel data having the same data configuration in Fig. 4.

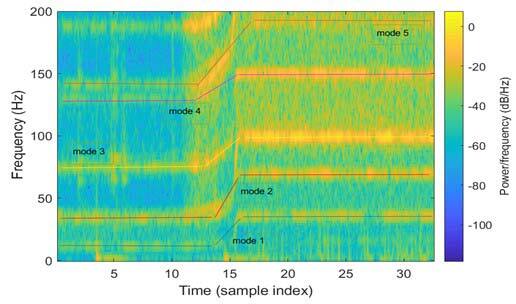
Fig. 4. Short-time Fourier transform of data

It has been shown that the proposed method is a powerful technique in monitoring natural frequencies. In terms of identification, the frequencies are accurately identified thanks to the autoregressive parametric method. Moreover, with the proposed updated algorithm, they are both qualitatively and quantitatively tracked and monitored in varying dynamic systems, such as non-stationary vibrations.

Conclusion

A method to update parameters over time and model order has been presented in this paper. The advantages of this method are that the inverse matrix is updated so that only the sub-matrices are calculated when the order increases or decreases, and it can be combined with time updates, providing an effective method to monitor modal parameters of a slow varying system, such as non-stationary vibrations. The sliding window technique is used in the multivariate autoregressive model to track modal parameter changes. The proposed method has been validated by real vibration cases using a plate emerging from water. Results show that the proposed method greatly reduces computational time and is a powerful technique in monitoring modal parameters for non-stationary vibration systems.

Additional Information

For more information on this research, please read the following paper:

Bui, T.-T.; Vu, V.H.; Liu, Z. 2022. “Modal analysis of slow varying non-stationary vibration by model updating with Schur complement.” Mechanical Systems and Signal Processing. Volume 162.